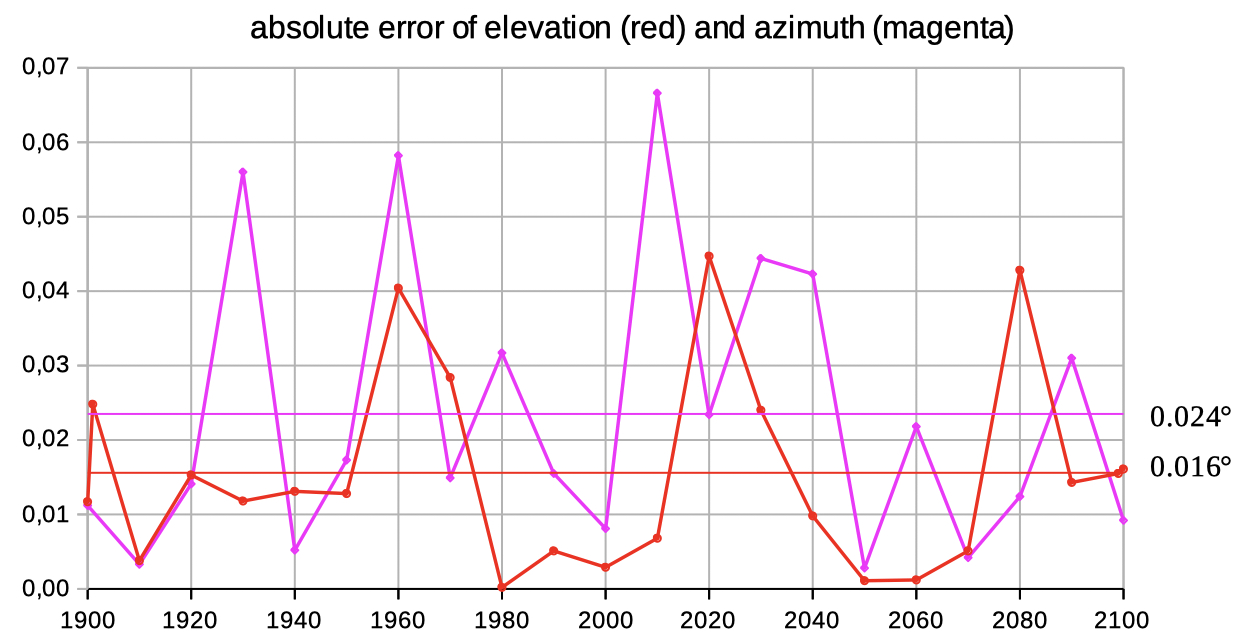
Reference: the 4 decimals of HORIZONS Web-Interface (NASA JPL)
Position and illuminated
fraction of the Moon by Spreadsheet
|
Input (red frames): 1) date and time |
| The spreadsheet is using an algorithm
(below in Java) from Montenbruck,
Pfleger: Astronomy on the Personal Computer: double T = (JD - 2451545)/36525; double eps = 23.4393-46.815*T/3600 double coseps = Math.cos(K*eps); double sineps = Math.sin(K*eps); double L0, L, LS, F, D, H, S, N, DL, CB; double L_Moon, B_Moon, V, W, X, Y, Z, rho; double ARC = 206264.8062 // rad to arcseconds L0 = frac(0.606433 + 1336.855225*T); // mean longitude of the moon, rad L = P2*frac(0.374897 + 1325.552410*T); // mean anomaly of the moon, rad LS = P2*frac(0.993133 + 99.997361*T); // mean longitude of the sun, rad D = P2*frac(0.827361 + 1236.853086*T); // diff. of longitudes moon-sun F = P2*frac(0.259086 + 1342.227825*T); // moon's distance from ascending node DL = 22640*Math.sin(L) - 4586*Math.sin(L-2*D) + 2370*Math.sin(2*D) + 769*Math.sin(2*L) - 668*Math.sin(LS) - 412*Math.sin(2*F) - 212*Math.sin(2*L-2*D) - 206*Math.sin(L+LS-2*D) + 192*Math.sin(L+2*D) - 165*Math.sin(LS-2*D) - 125*Math.sin(D) - 110*Math.sin(L+LS) + 148*Math.sin(L-LS) -55*Math.sin(2*F-2*D); S = F + (DL + 412*Math.sin(2*F) + 541*Math.sin(LS))/ARC; H = F - 2*D; N = -526*Math.sin(H) + 44*Math.sin(L+H) - 31*Math.sin(-L+H) - 23*Math.sin(LS+H) + 11*Math.sin(-LS+H) - 25* Math.sin(-2*L+F) + 21*Math.sin(-L+F); L_Moon = P2*frac(L0 + DL/1296E3); B_Moon = (18520.0*Math.sin(S) + N)/ARC; // equatorial coord. CB = Math.cos(B_Moon); X = CB*Math.cos(L_Moon); V = CB*Math.sin(L_Moon); W = Math.sin(B_Moon); Y = coseps*V - sineps*W; Z = sineps*V + coseps*W; rho = Math.sqrt(1.0-Z*Z); DEC = (180.0/Math.PI)*Math.atan(Z/rho); RA = (24.0/Math.PI)*Math.atan2(Y,X+rho); if (RA<0) RA = RA + 24.0; ------------------
sinElev = Math.cos(K*LAT)*Math.cos(K*DEC)*Math.cos(K*HA) +
Math.sin(K*LAT)*Math.sin(K*DEC);T = (JD - 2451545)/36525 // JD =
Julian Day
LST = 280.46061837 +
360.98564736629*(JD-2451545) + 0.000387933*T^2 -
T^3/38710000 + LONG
LHA = local hour angle = LST - 15*RA // LST = mean local sidereal time elev1 = Math.asin(sinElev)/K The columns right of AF are computing the parallax of the Moon (elev = elev1 - p) column AG is the equatorial horizontal parallax P lunar parallax: sin(p) = R·sin(P)·cos(elev), R=0.9983+0.0017·cos(2·LAT) elev = elev1 - p The atmospheric refraction r is computed by 1.02/(60*tan(K*(elev+10.3/(elev+5.11)))) The observed elevation is elevRefr = elev - r The illuminated fraction of the Moon is calculated by (1+cos(i))/2 |

|
|
|
Die Zeitgleichung: Eine einfache Formel zu Sonnenaufgang und Untergang General
Solar Position Calculations (PDF) MICA (Multiliyear Interactive Computer Almanac 1800-2051), US Naval Observatory 2011, no longer published |