Position of the Moon
START
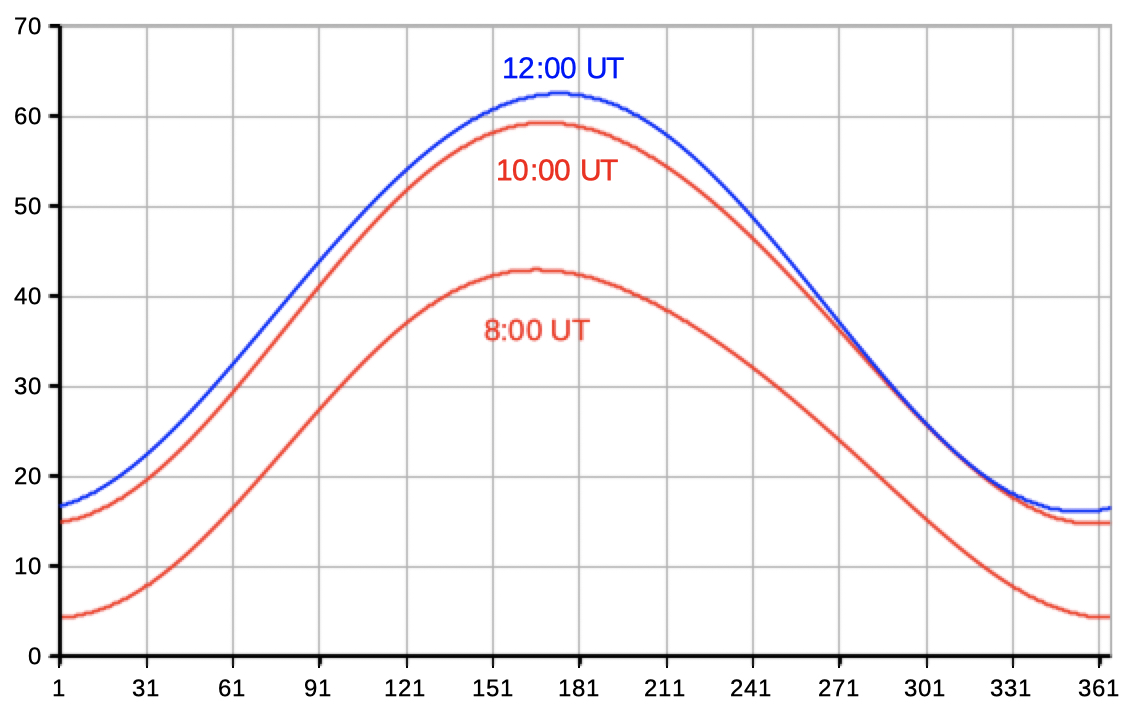
the Sun for a month the Sun for a day
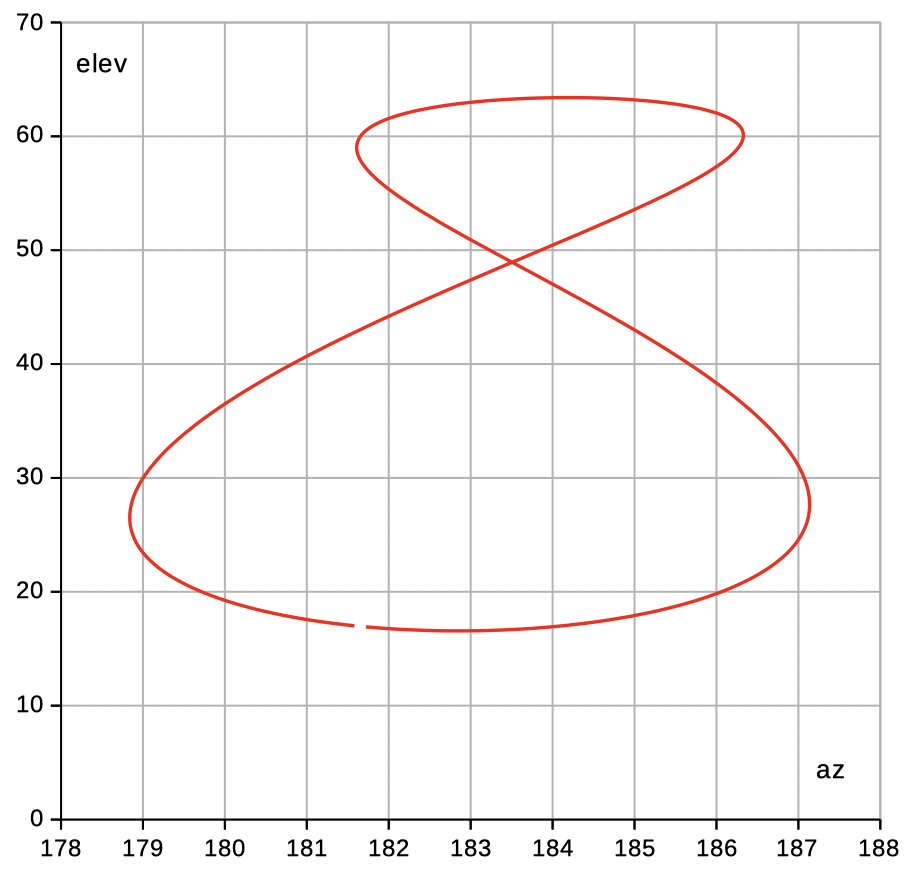
The Analemma of the Moon
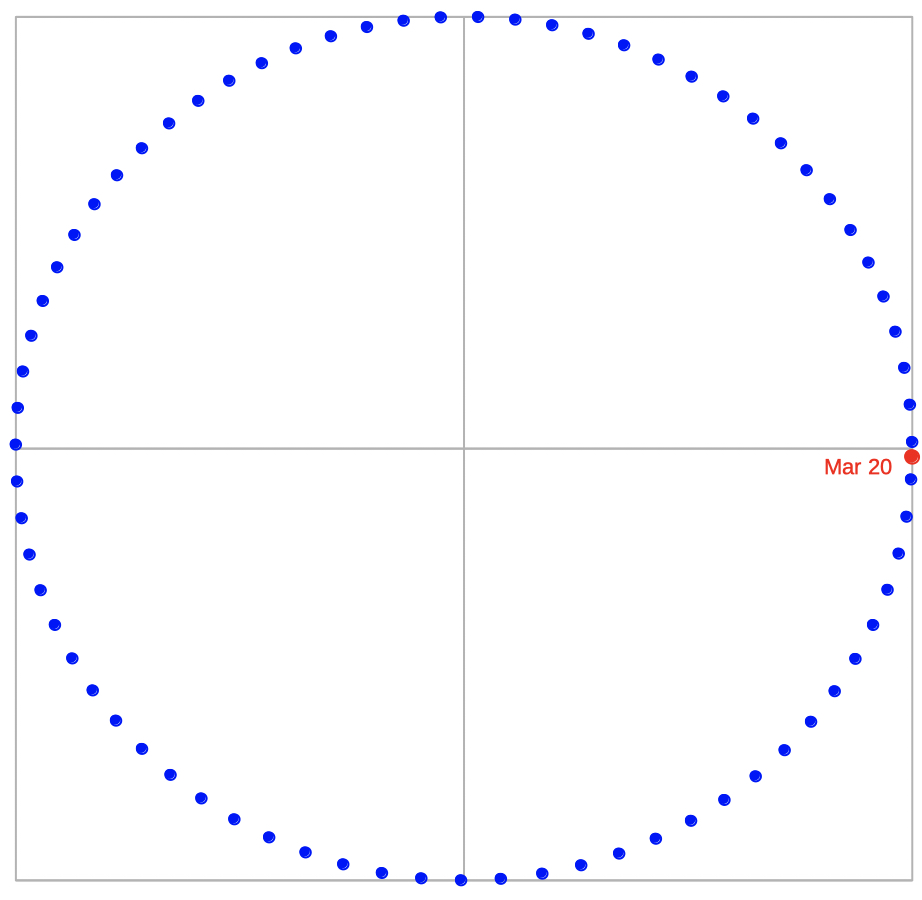
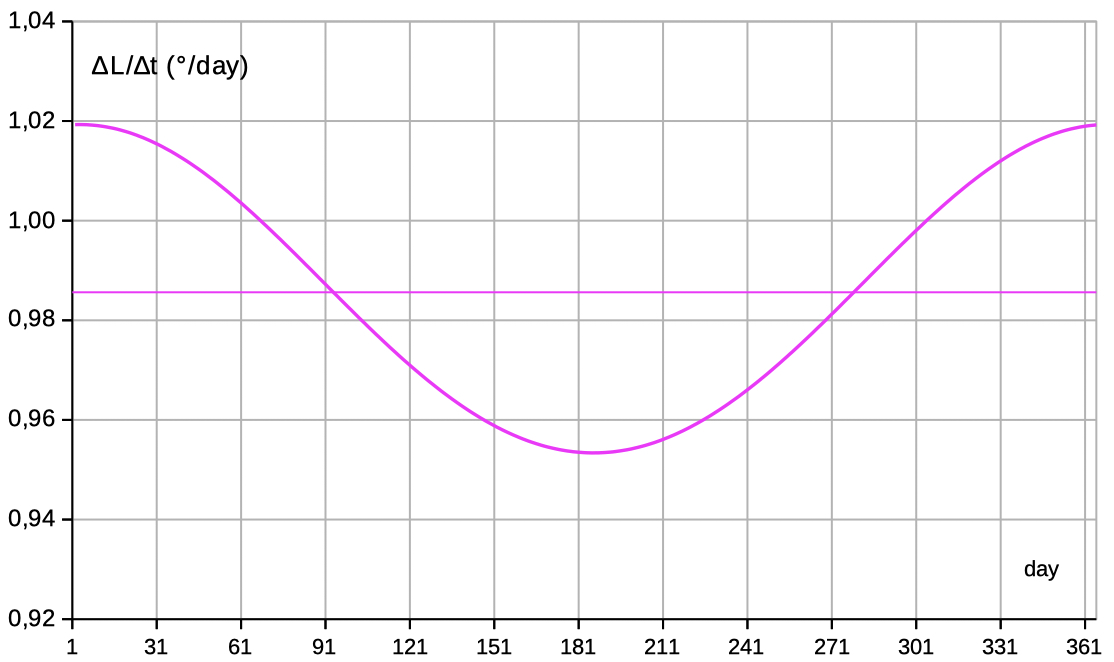
Position of the Sun by
Spreadsheet
for a year
download
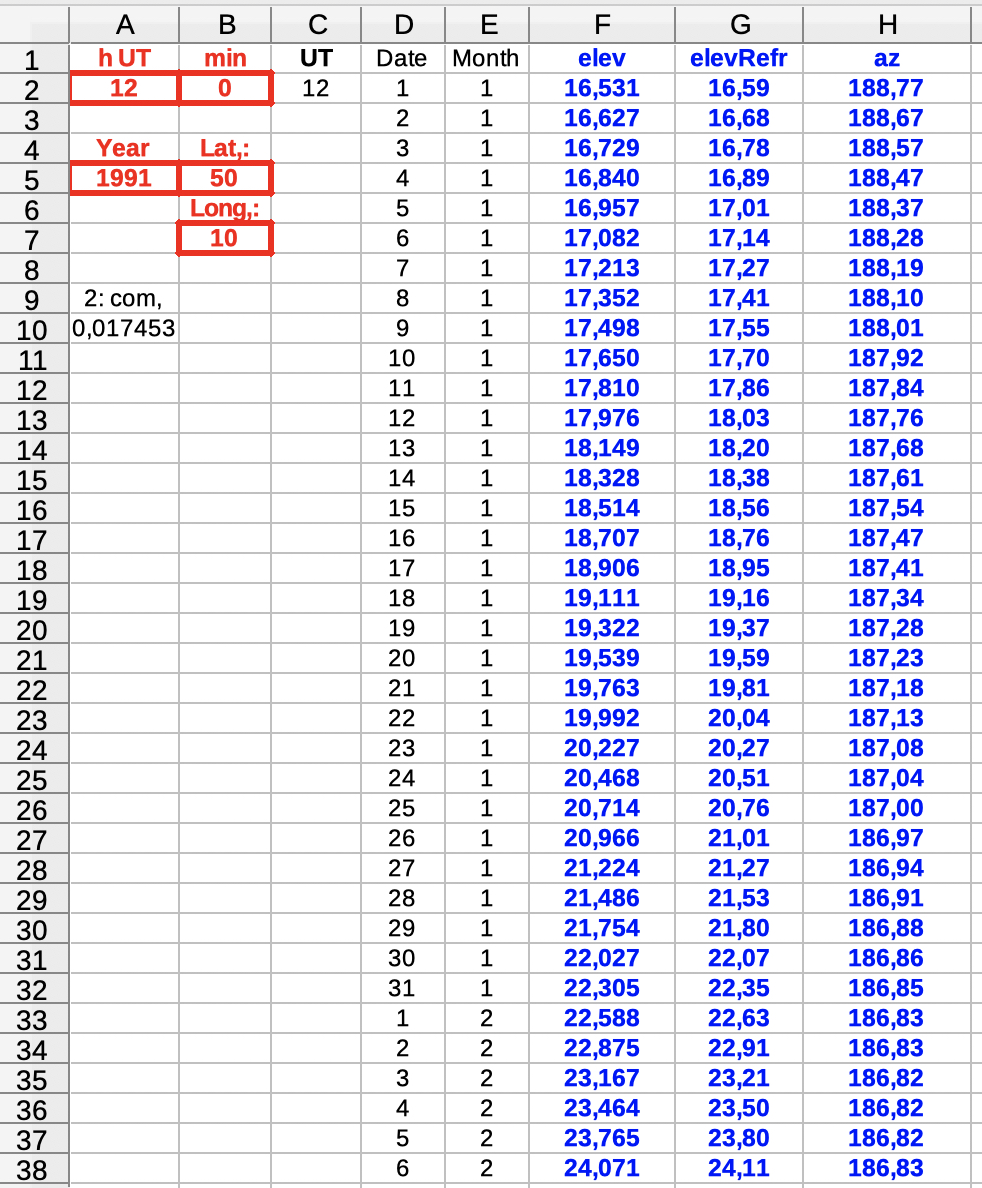
| Select the table 'input': | |
|
Input (red frames): 1) hour UT, min |
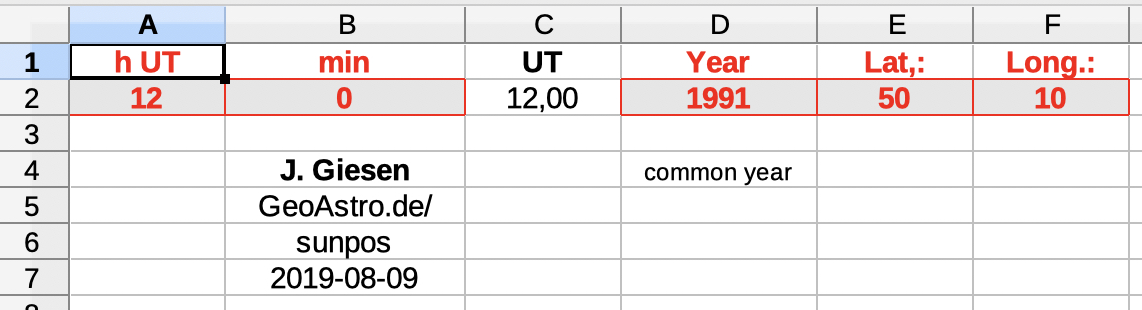 |
| The table calc performs the calculations, using a lot of auxiliary variables. It should be neglected. | |
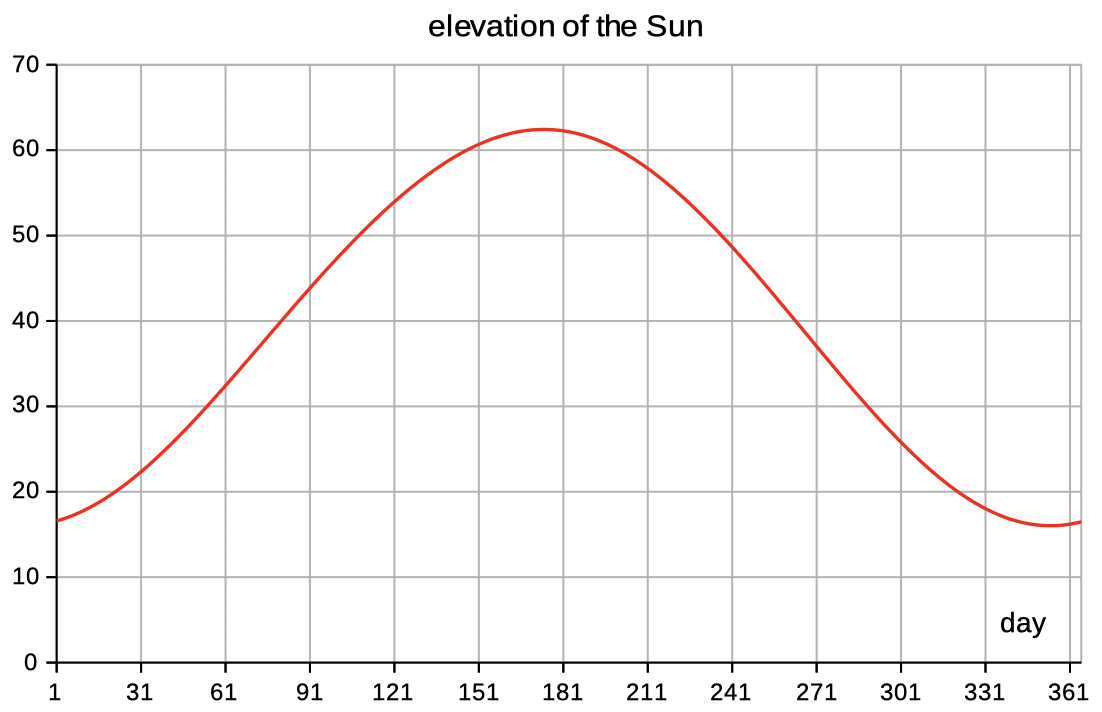
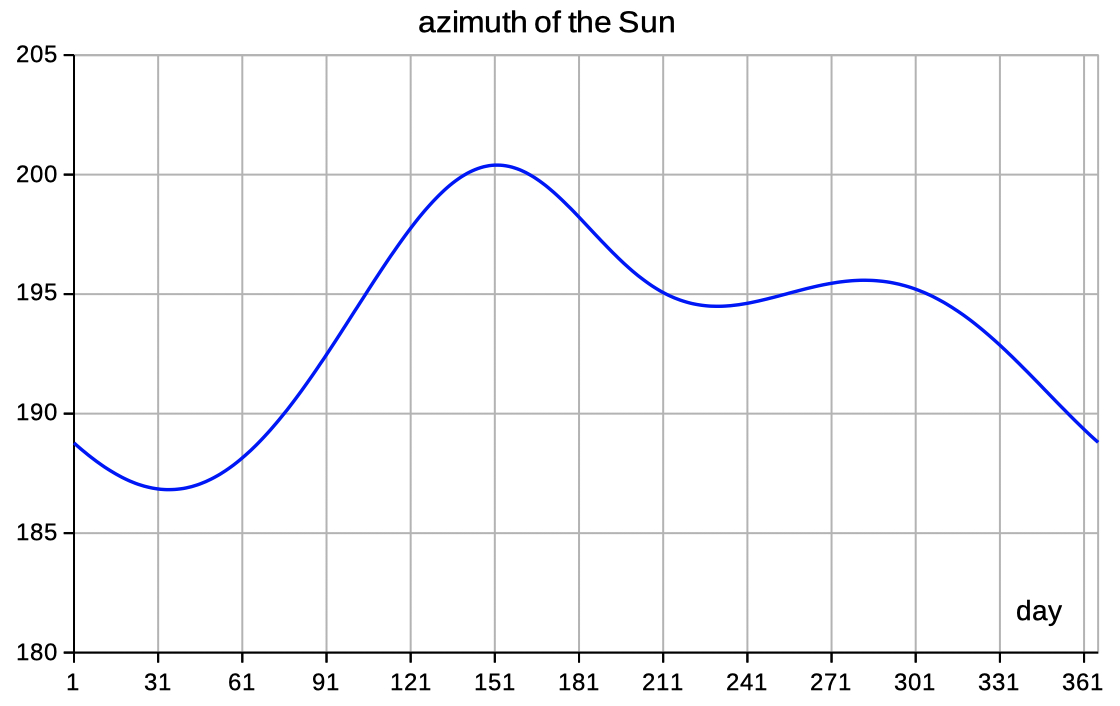
| Select elev az to see data and diagrams of elevation and azimuth. | |
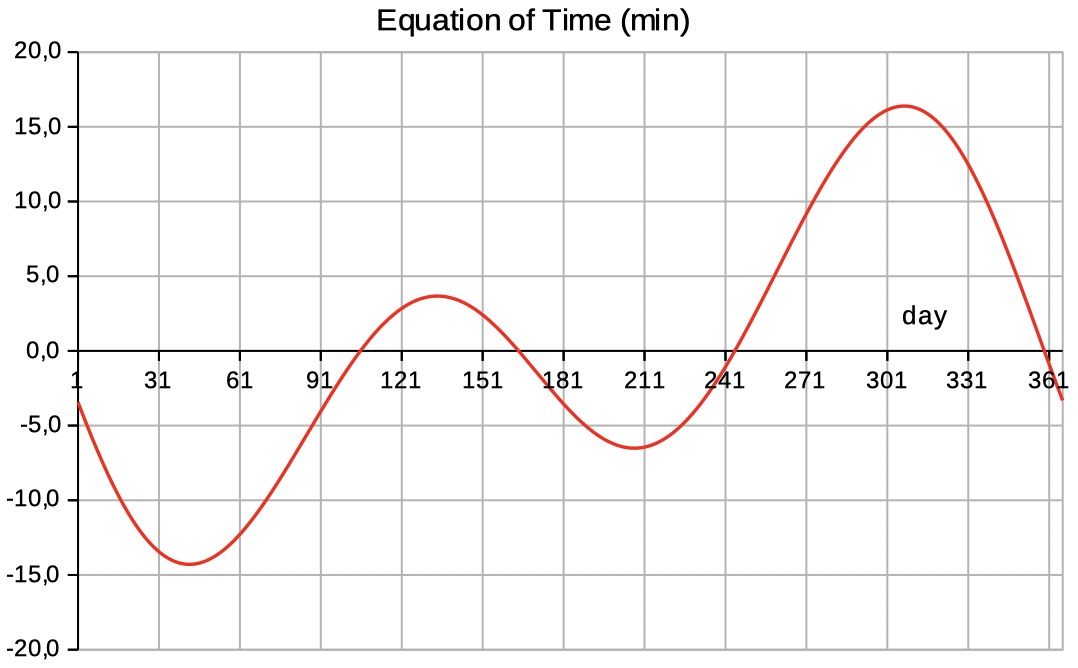
| Select E o T for data and diagrams of the Equation of Time. | |
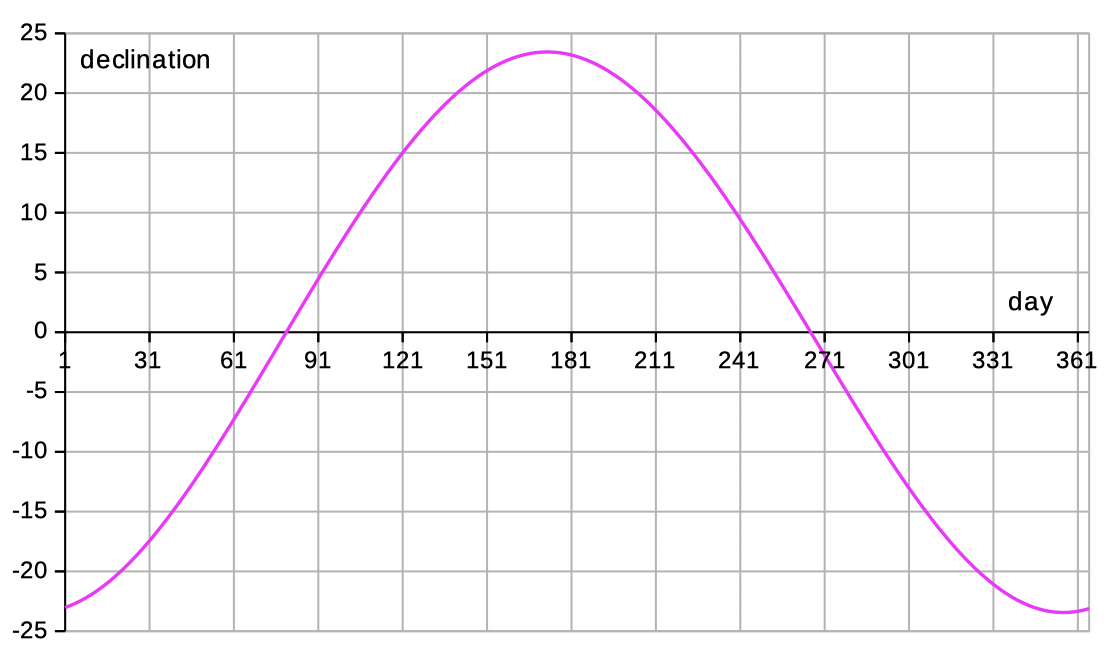
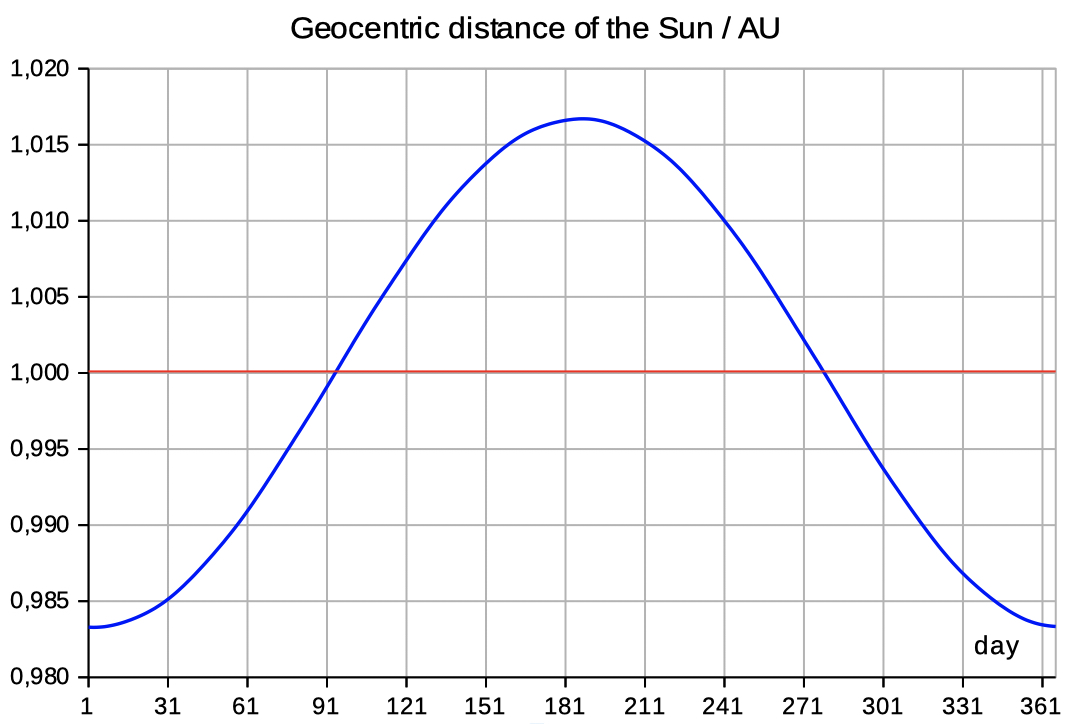
| Select declin dist to see data and diagrams of the declination and distance. | |
| Select orbit to see data and a diagram of the ecliptic orbit. |