|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
The applet is computing the apparent distance of the Earth from the Sun (kilometers and Astronomical Units) using the 409 most important of 997 terms of the VSOP87 planetary theory. In 1850 to 2050, the mean absolute error of the Sun-Earth distance, compared with MICA, is 1.9·10-7 AU = 28 km, using the conversion 1 AU = 149,597,870 km (details below). The times of perihelion and aphelion are accurate within about 0.5 hour, and the right ascension and the declination (using fewer terms) are accurate within about 1''. Select "Anomalistic"
from the "Details" menu:
The
anomalistic period of the Earth is the time
that elapses between two passages at its
perihelion. There
are large
deviations of
the interval between
perihelion passages
(anomalistic period), caused
by the Moon deforming the path
of the Earth's center (Meeus).
more details below 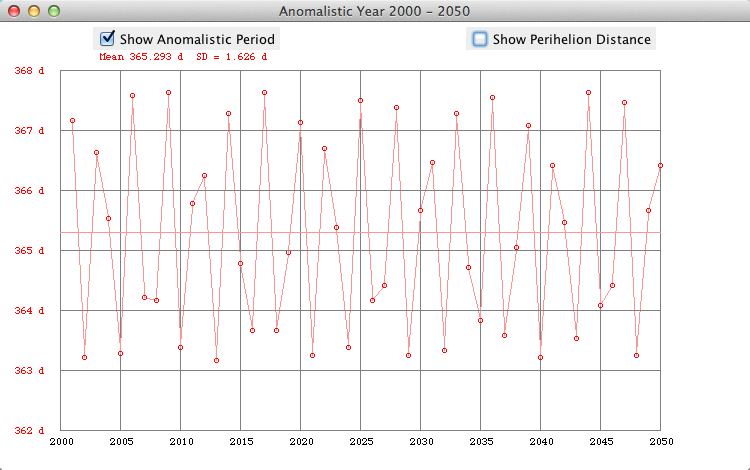 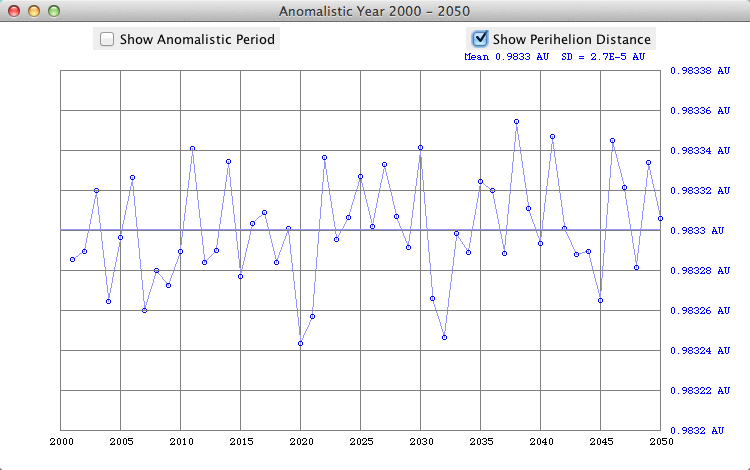 Select "Data Table" from the "Details"
menu:
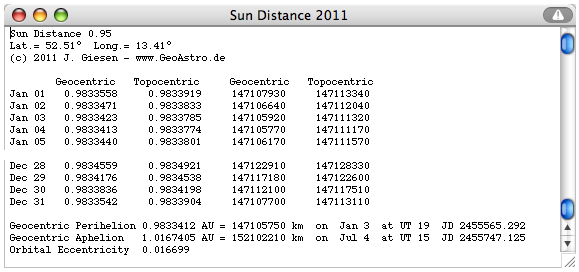 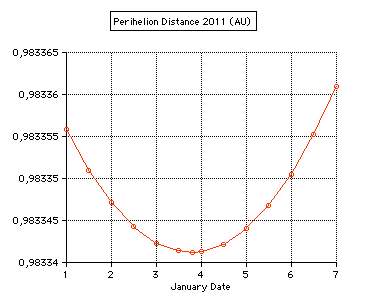 Perihelion 2011 occurs on Jan 3 at 19 UT (0.9833412 AU). 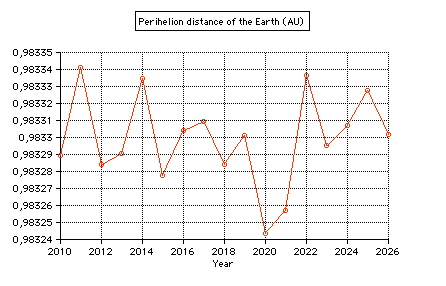 Geocentric perihelion distance 2010 -
2026
computed by MICA (Multiyear Interactive Computer Almanac by US Naval Observatory)
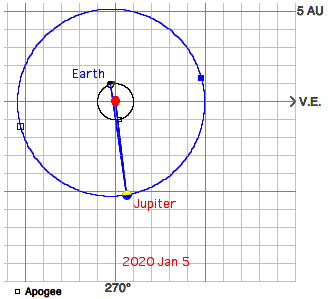 The small perihelion distance of the Earth in 2020 and 2021 is due to the conjunctions of Jupiter with the Sun (2019 Dec 27, 2021 Jan 29). Perihelion occurs between Jan 2 and Jan 05 (mean date is Jan 4.0):  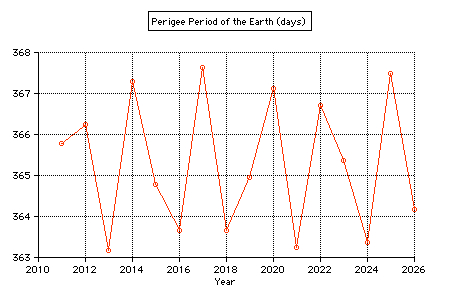
The ecliptical longitude of the perihelion is advancing by about 3.3° from 1900 to 2100, making one complete cycle in 22,000 to 26,000 years: 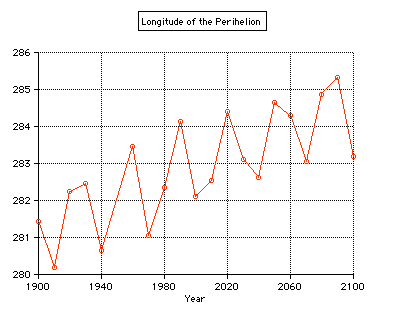 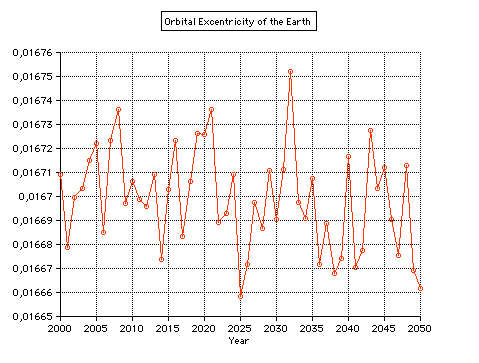
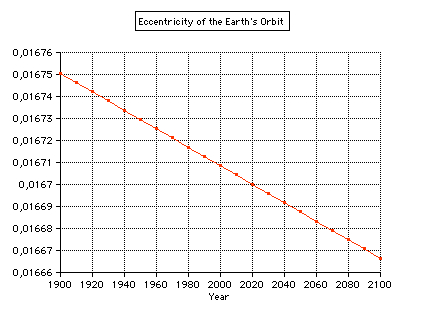 The eccentricity of the Earth's orbit 1900 - 2100 according to Meeus (Astronomical Algorithms, Willmann-Bell) is decreasing by 0.000,042 per century (0.0167,086 in 2000). In 29,450 there will be a minimum of 0.002281: 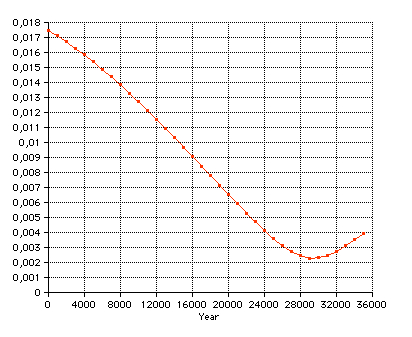 More details about long-period variation of the Earth's eccentricity 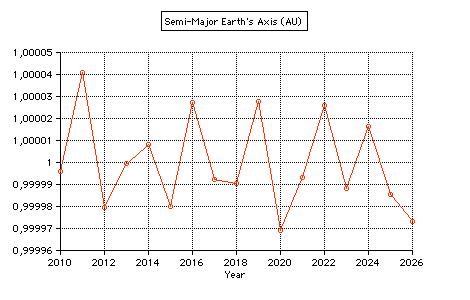 Select "Difference" from the "Details" menu: Showing the second differences dn of daily distances rn: dn = (rn+1 - rn) - (rn - rn-1) = rn+1 - 2rn + rn-1 which is an approximation of the second derivative of the r(t) function. It is about zero near the equinoxes where the orbit is almost circular (dn=0). 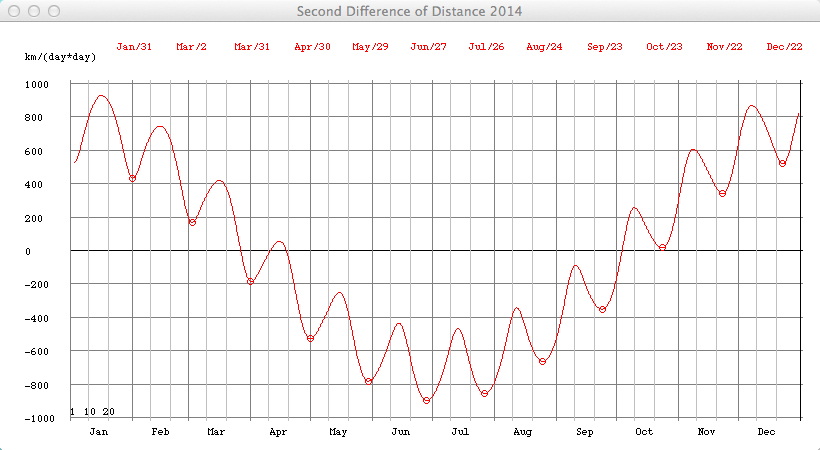 The local minima of dn occur at (near) New Moon. Select "Orbit" from the "Details" menu: 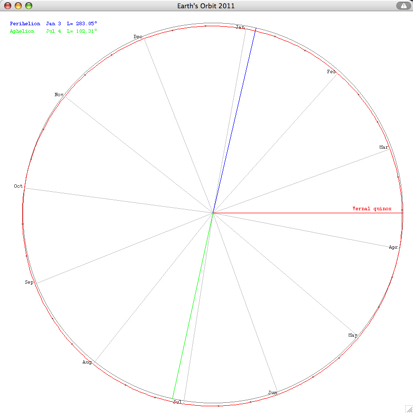 An eccenticity of 0.0167 and a radius of 380 pix yields a difference between perihelion and aphelion distance of 12 pix. Marks for the date of the month:   This checkboxes is showing the magnified radius (magenta), concentric gray circles at 0.995 AU, 1 AU, and 1.005 AU  The local radius (cyan) is computed from 3 adjacent points Pn-1, Pn, Pn+1, using rectangular coordinates computed from the radius r and the ecliptical longitude L. Cyclic variations is due to the Eart's moon. Local minima occur at new moon. VSOP Theory VSOP 87D: heliocentric ecliptic spherical coordinates for the equinox of the day The VSOP
theorie is computing the Sun-Earth distance R
from the Julian Day JD by the sum of series R0,
R1, R2, R3,
and R4:
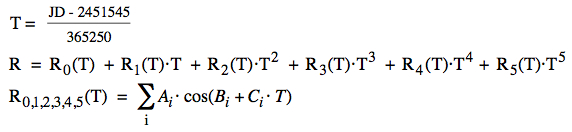 The coefficients Ai of R0 (526 terms) behave like this (in units of AU): 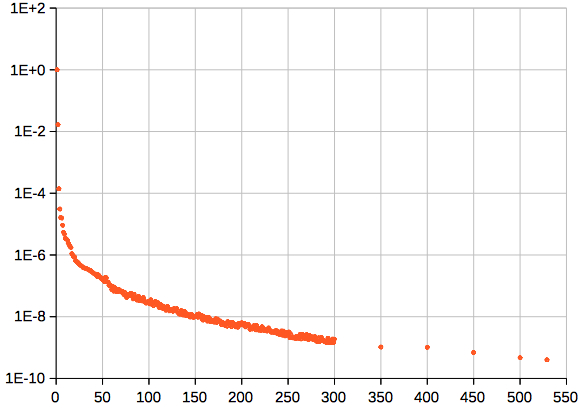 Mean absolute error of R (in units of AU), 1900-2050: 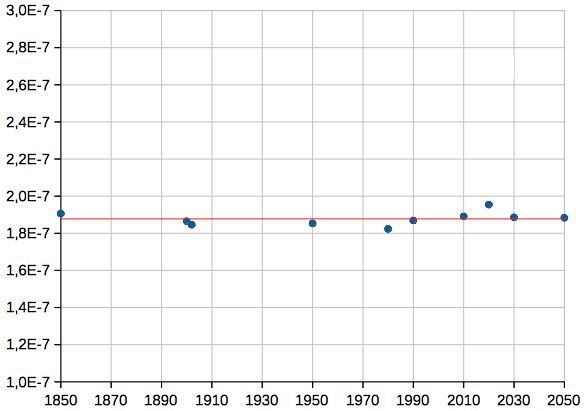 Above: mean error (12 positions per year), and standard deviation: (1.87 ± 0.80)·10-7 AU, or (28 ± 12) km Perihelion of the Earth: There
are large
deviations of
the interval between
perihelion passages of the
Earth (anomalistic period),
caused by the Moon deforming
the path of the Earth's center
with respect to a rigorously
elliptical orbit [mean
perihelion] (Meeus).
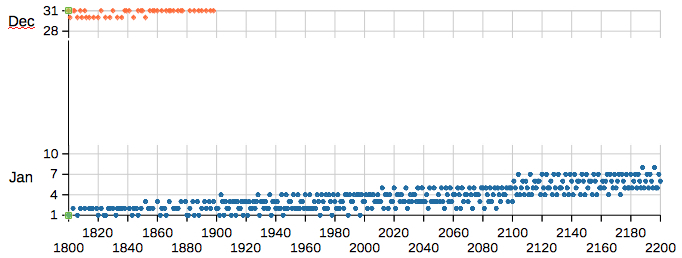 The last time of perihelion in December was in 1898, on December 31 at 21 UT. 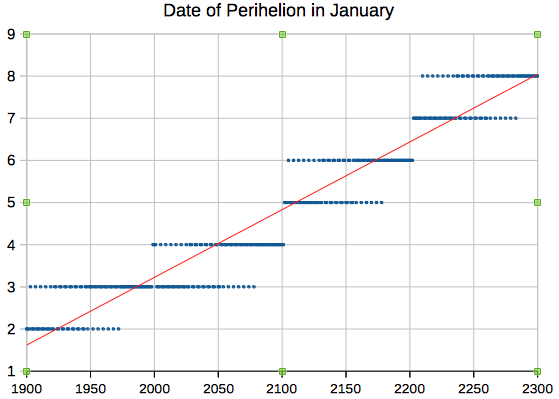 The
date of the mean perihelion, computed by
Meeus' algorithm (Meeus),
is increasing by about 1.6 days per century,
from December 26-28 near 1600 to January
10-13 near the year 2500.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Visit my page: The Moon: orbit and phases
|
|
|
Secular variations of the planetary
orbits (Wikipedia) EARTH - Heliocentric Distance And
Light Time Table Geocentric
Positions of Major Solar System Objects and Bright
Stars |
| Software |
| MICA,
Multiyear Interactive Computer Almanac (1780-2050); US Naval Observatory; Version 2.2.2 |
| Books |
| Meeus, Jean:
Mathematical Astronomy Morsels; Willmann-Bell,
Richmond, Virginia; Chapter 27: On the passages of Earth in perihelion. Meeus, Jean: Astronomical Algorithms; Willmann-Bell, Richmond, Virginia; Chapter 37: Planets in Perihelion and Aphelion. |
©
2011-2023 J. Giesen
![]()
Last
modified: 2023, Oct 12


