|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Atmospheric Refraction Applet
Apparent Flattening of the Sun
|
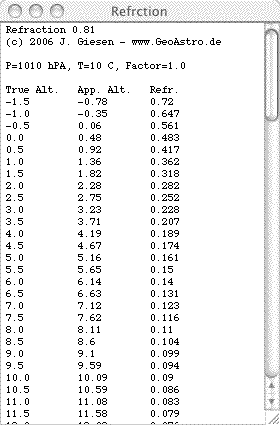
The true elevation angles of the Sun are not corrected for atmospheric refraction, which is bending the light while passing through the Earth's atmosphere. The effect of refraction depends on atmospheric conditions (pressure, temperature, relative humidity) and on the wavelength. For mean conditions (P=1010 hPa, T=10°C, yellow light) the refraction R is calculated by Saemundsson's formula (Meeus, Astronomical Algorithms): 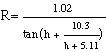 h is the true (airless) elevation in degrees, R is in minutes of arc. The apparent (observed) elevation is h+R. Taking into account variations of the pressure P (hPa) and the temperature T (°C), R should be multiplied by the approimate faktor (Meeus, Astronomical Algorithms): The amount of refraction increases by
about 1% for every 3 °C colder, and by about 1% for every 9 hPa higher
pressure. As a consequence of the refraction, the solar disc seems to be flattened near the horizon. At runrise, when the apparent lower limb is just on the horizon, the apparent vertical diameter of the Sun is 26.9', and the apparent flattening ratio is For my photo  the ratio of flattening is about 0.86. |
Select
"Graph:
Refraction" from the "Details" menu:
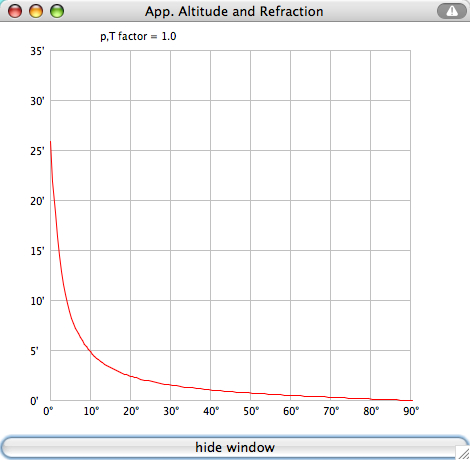
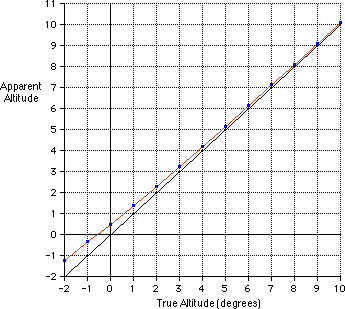
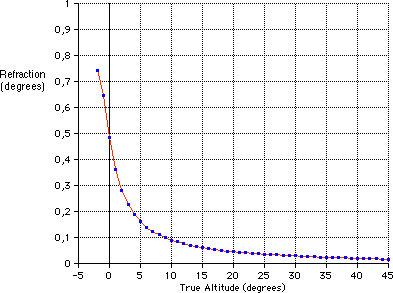

Altitude correction (arcminutes): apparent alt. = true alt. + correction.

Apparent
flattening
ratio of the Sun.
(c) 2006-2023 J. Giesen
Updated:
2023, Oct 06