|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Random Walk Applet
1 dimension: The blue point is moving on a line with integer coordinates: The 2 directions of a single step: x+1, x-1 2 dimensions: The blue point is moving in a plane with integer coordinates:  The 4 directions of a single step: x+1, x-1, y+1, y-1 |
| select from the menu |
|
| button starting a single walk, maximum of n=1000 steps, the diagram at the bottom is showing the distances d(n) button to stop the walk |
1 dimension:
An interesting question arising in the
study of random walks concerns
the probability of returning to the initial position
(origin, "equalization").
The probability P(n) of return to origin at step n (n even) is:

For large n (even):
![]()
Graph of the first (strict) formula:
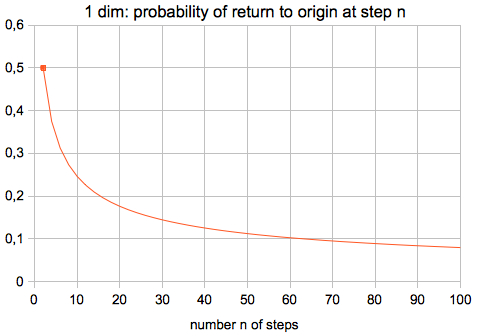
---
Applet results:

The total number of
returns to origin (within a fixed number n of steps) is
proportional
to the number N of walks:
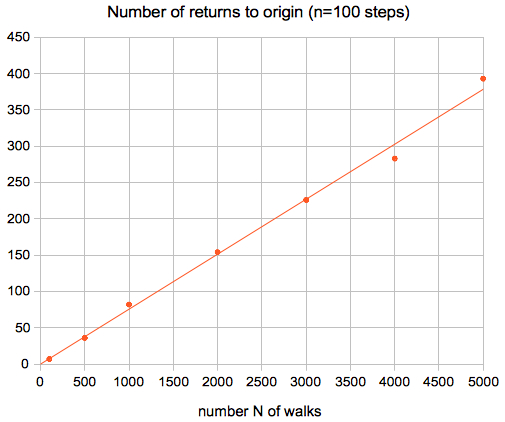
The probalibity for n=100 steps is 0.076
2
dimensions:
Example:
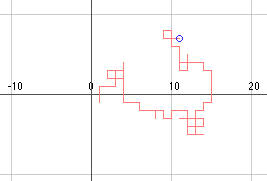
100 steps, final position (11|7),
the distance from origin is d = sqrt(x2+y2) = 13.04
-----
The probability of return to origin at step n (n even):
and for large n:
In 2 dimensions the probability is, of course, the square of
the one in 1 dimension, requiring x=0 AND y=0
Graph of the first (strict) formula:
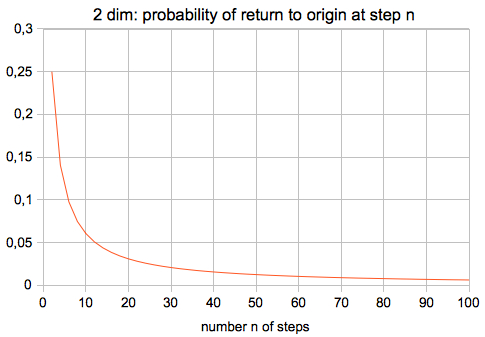
---
Applet results:
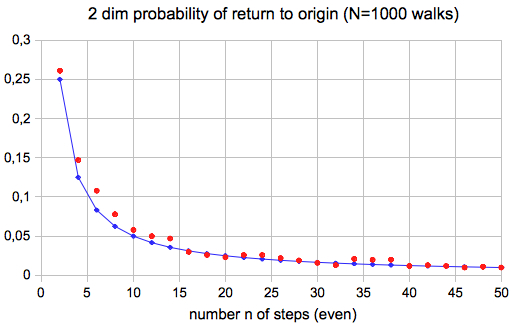
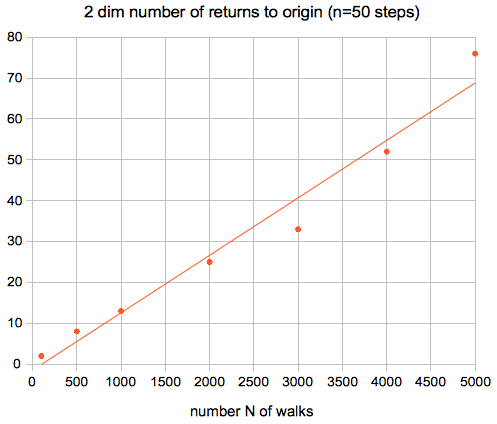
The probalibity for n=50 steps is 0.014
Statistical analysis
| button starting a set of N walks |
|
| the numbers of steps and walks can be selected from the menus |
The mean squared distance is proportional to the number n of steps:


| Books |
| Küppers, Bernd-Olaf: Die Berechenbarkeit
der Welt, Grenzfragen der exakten Wissenschaften. S.
Hirzel, Stuttgart 2012. Entropie und Zeitstruktur, S. 200-210 Eigen, Manfred, and Winkler, Ruth: Das Spiel, Naturgesetze steuern den Zufall. Pieper, München 1975. Kapitel 4:Statistische Kugelspiele |
|
|
| Random
Walk--1-Dimensional (Wolfram MathWorld) Random Walk--2-Dimensional (Wolfram MathWorld) A 1D Random Walk Visits The Origin Infinitely Often |
Updated: 2023, Oct 06