Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

Der Sonn' entgegen... "Eine halb astronomische, halb geografisch-geodätische Aufgabe" von Arno Schmidt Peter rüttelte herrscherlich sein Gabelzepter über die Flämmchen, die sogleich gefällig zischelnd höher wucherten; stieß die Zinken in den Boden; drapierte die verschränkten Arme dicker auf den Stiel, und erkundigte sich tiefsinnig: „Wo käm’ man da eigentlich hin? Wenn man immerfort ‚Der Sonn’ entgegen‘ ginge?“ „Von morgens an? Na, da würd’s’De abends wieder am Ausgangspunkt sein“, entschied ich, voreilig wie immer… „Nein. Neinein“, sagte er: „Davon kann gar keine Rede sein, daß man abends wieder am Ausgangspunkt wäre. Das ist sogar…eine ziemlich komplizierte Angelegenheit… Zuerst ginge man nach Osten. Dann nach Süden ausholend…Dann, im Laufe des Nachmittags, Süd-West…und schließlich nach Westen: immer der Sonn’ entgegen“. „Am einfachsten wäre’s, man führte das…Experiment einmal praktisch durch“… „Wie, zum Beispiel, der Sonn’ entgegen zu gehen… Ich sag’ Dir bloß das Eine: wenn ich unterwegs an einem Strunk eine KIEFERNGLUCKE erblicken sollte: die wird geerntet!“ „Kannst Du Dir nicht Sparassis ramosa merken, Peter?“ tadelte Fritz…: „Eine Unterbrechung kommt selbstverständlich überhaupt nicht infrage. Und wenn uns ein ganzer Harem verlockend in den Weg tänzelte!“ Quelle: Arno Schmidt, Der Sonn' entgegen ..., in: Werke. Bargfelder Ausgabe. I/3, S. 293-311. Niederschrift des Textes: 1960, erstmals erschienen in dem Band "Kühe in Halbtrauer", Stahlberg Verlag, Karlsruhe 1964. Pursuing the Sun A mathematical astronomy problem From a point on the Earth, a walker starts at sunrise, walking at a constant speed always in the direction of the Sun, and ending at sunset. What is the path ? Bargfeld (Germany, 52.7039° N, 10.3459° E) was the residence of Arno Schmidt (*1914, +1979).

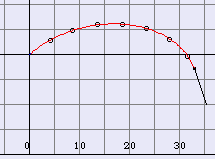
	Opening this page the applet is showing the complete path from sunrise to sunset. To walk stepwise, press the button "Clear", and then press the key "+": The time will increase by 1 minute. Pressing the key "h", the time will increase by 1 hour. The speed is preset to v=5 km/h, and can be changed.
	Use the keys d, or m to increase the date, or month.
	Select from the menu to change the speed v, or the time step dT.
	Select "Positions on/off" from the menu to draw the position at every hour after sunrise.
The calculation is performed step by step, using the time interval selected. For sunrise and sunset the refraction of light is taken into account, as well as the (small) change of the declination during the walk.
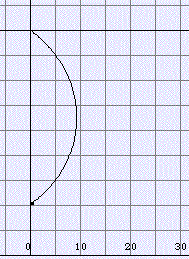
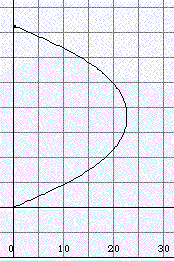
	Latitude 50° N, summer solstice (δ=23.44°), daylight 16h 22m, v=5 km/h, path 81.7 km (dT=5 min)
	Latitude 50° N, equinox (δ=0°), daylight 12h 09m, v=5 km/h, path 60.9 km (dT=5 min)
	Latitude 50° N, winter solstice (δ=-23.4°), daylight 8h 04m, v=5 km/h, path 40.4 km (dT=5 min)
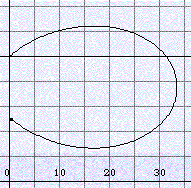
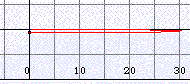
	Latitude 0° N (equator), summer solstice (δ=23.4°), daylight 12h 07m, v=5 km/h, path 60.8 km (dT=5 min)
	Latitude 0° N (equator), equinox (δ=0°), daylight 12h 06m, v=5 km/h, path 60.8 km (dT=5 min)
	There is a small difference between the curves for the step size dT=1 min and dT=10 min.

Numerical results: 2006, June 21, 50° N, 10° E, v=5 km/h,
the accuracy increases using a small stepsize dT:

dT / min	East / km	North / km	South / km
60	35.23	7.68	-16.78
30	34.35	6.81	-17.63
20	34.02	6.53	-17.90
10	33.69	6.26	-18.17
5	33.53	6.12	-18.30
1	33.41	6.02	-18.41

At Bargfeld, on August 1, the total path length is 77.83 km, walking v=5 km/h.







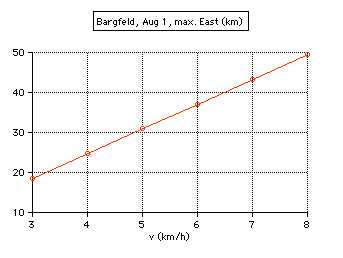
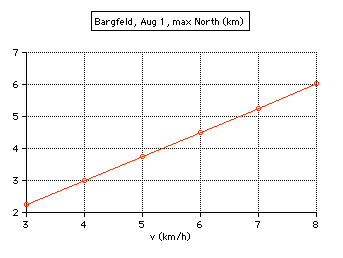
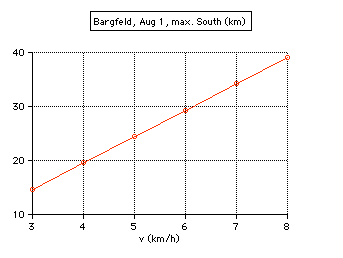
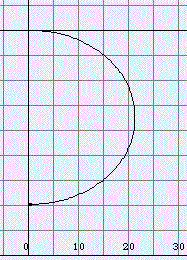
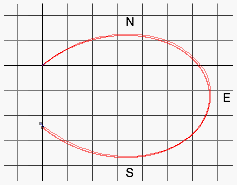
A sophisticated analysis of the curve:
The evolute of a given curve is the envelope of the normals to it.
This can also be thought of as the locus of the centres of curvature.
The evolute of a circle would be it's center.



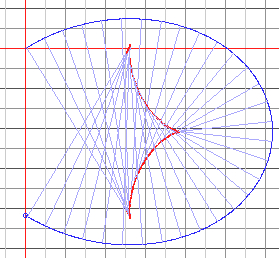
The evolute (red curve) at Bargfeld on August 1.
Choose "Evolute from the "Select" menu.

Web Links

Der Sonne entgegen (Wikipedia) Jean Meeus: Pursuing the Sun. l'Astronomie, Vol. 116, May 2002, pages 206-209, und in: Jean Meeus: Mathematical Astronomy Morsels III, Chapter 53, Willmann-Bell, 2004. Arno Schmidt Stiftung, Bargfeld H. Joachim Schlichting: Immer der Sonne entgegen, Spektrum der Wissenschaft, August 2013, S. 58-60 http://heft.spektrum.de/alias/dachzeile/immer-der-sonne-entgegen/1199287 U. Finkenzeller: Sterne und Wortraum Arno Schmidts Die Werke des ebenso bedeutenden wie eigenwilligen Schriftstellers sind voller Wortspiele, Andeutungen und Hinweise auf astronomische Themen. In: Sterne und Weltraum, 8/2007, Seite 48-54. Berthold Schuppar: Der Sonn' entgegen - Ein mathematisch- astronomisches Problem, gestellt von Arno Schmidt. Didaktik Math. 20 (1992), 89-111. Wolfgang Müller: Der Lösung entgegen - Arno Schmidts "Wanderkurve" in erster Annäherung. Bargfelder Bote, Materialien zum Werk Arno Schmidts, Lfg. 89-90/April 1985, S. 12-23. Susanne Neuhäusler: Verfolgungsprobleme mit Java Radiodrome (Wikipedia) Pursuit Curve (Wolfram MathWorld) Andrew J. Simoson: Pursuit Curves for the Man in the Moone Tractrix (Wikipedia) Pursuit Curves (K. Steiner, J. Franchi, PDF) National Curve Bank, A Simulation of Pursuit Curves Ulrich Goerdten: Arno Schmidts 'Ländliche Erzählungen'. Sechs Interpretationen, Bangert & Metzler 2011, ISBN 978-3-924147-63-1. Inhaltsverzeichnis darin: Mehr als der Augenschein vortrügt. Bemerkungen zu Arno Schmidts Erzählung 'Der Sonn entgegen'. S. 105-136 Arno Schmidt: Das schönere Europa Zur Erinnerung an die erste große wissenschaftliche Gemeinschaftsleistung unserers Kontinentes, den Venusdurchgang von 1769.

(c) 2006-2013, J. Giesen

Updated: 2023, Oct 04