Sieve for Prime Numbers by a Parabola

Home:

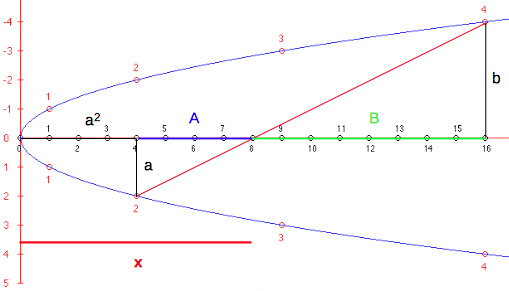
The page "Crible géométrique (hyperbole)" by Jean-Paul Davalan inspired me to write the interactive Java applet below.

On the rectangular parabola x = y² the points { (i² , i), i integer, i >1 } and { (k² , -k), k integer, k >1 } are marked and joined by a line crossing the horizontal x axis.

The points of intersection are (i · k, 0), indicaomittingting the product, the prime numbers

{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, ...}

if i≠1 or k≠1.

This sieve was created by Yuri Matiyasevich and Boris Stechkin.

The construction also interprets the multiplication of real numbers.

	Select the maximum value of x on the horizontal axis.
	Select the number of lines to be drawn from each point on the parabola.
	Pressing the "clear" button erases all lines. Click on a number on the parabola (with cursor set to cross hair) to draw lines, or press "draw lines" to redraw all.
	You can add the lines using the click mode.

Web Links

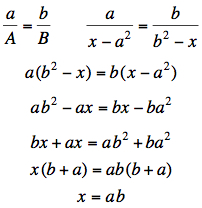
A visual Sieve for Prime Numbers (Yuri MATIYASEVICH and Boris STECHKIN)

A Parabola Sieve for Prime Numbers (Wolfram)

Catching primes (Abigail Kirk)

Le crible géométrique de Matiiassevitch (Therese Eveilleau)

2017-2023 J. Giesen

updated: 2023, Oct 06