|
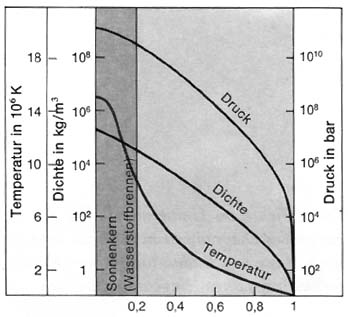
Temperatur im Inneren der Sonne
Pressure, density and temperature inside
the Sun
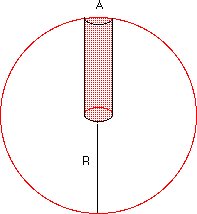
To be in a steady state the thermal gas pressure of the star must be in equilibrium with gravitation. First, we estimate the gravitational pressure in the centre of the star:
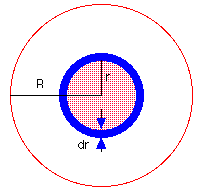
p = F / A = G·ρ·M / R The ratio p / ρ is given by On the other hand, the pressure p of the star, considered as an ideal gas of N atoms of mass mA, is ( k = Boltzmann constant, T = abs. Temperature) With ρ = N·mA / V we get the ratio To be stable the following equation must be valid: For the temperature T we get
mA
= 1.7·10-27 kg M =
2·1030 kg k =
1.4·10-23 J / K R =
7·108 m constant of
gravitation mass of hydrogen
atom mass of the Sun
Boltzmann
constant radius of the
Sun T = 2.3·107 K = 23,000,000 K A more realistic value is 15,000,000 K (surface temperature: 5800 K) The pressure in the centre of the Sun with the mean density ρ = 1.4·103 kg / m3 is The real value should be greater because the density increases towards the center.
Our Sun and Stellar
Structure (Bakersfield College)
The Sun's Power Source
(Bakersfield College) How the Sun Shines Last update 2020, Feb 27 |