|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
The Problem of the Earth's Shape
Simulation Applet
| In the late 17th and early 18th century
there was a debate about the shape of the Earth:
In his "Principia", appearing in 1687, Isaac Newton described the
Earth as flattened at the poles (left) by the
force caused by the rotation of the earth. French astronomers (Cassini e. a.) affirmed to have proved the opposite by arc measurements, i. e. the Earth is elongated at the poles (right). 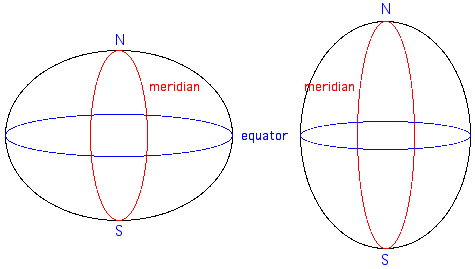 In order to
resolve the disagreement, the French Academy
of Sciences, authorized by King Louis XV,
equipped two expeditions to
perform measurements along a
meridian arc at places as distant as possible:
one to the equator (Peru), the other to the
high North
(Lapland).
In 1735 Louis Godin, Charles-Marie de La Condamine, and Pierre Bouguer, members of the French Academy of Sciences, accompanied by Joseph de Jussieu, Jean Séniergue, Jean Godin des Odonnais, Jean Verguin, three assistants (Couplet, de Morainville, Hugot), and the Spanish officers Jorge Juan and Antonio de Ulloa, sailed to Peru (Spanish colony since 1542, now Ecuador). In the high Andes they triangulated 3 degrees south of Quito with high precision, completing the measurements as late as 1744. There are some fascinating books describing the adventures of the expedition. Four of the members did not survive it: Couplet, Séniergue, Morainville, Hugot. The Lapponian expedition, led by Pierre-Louis Moreau de Maupertuis, lasting one year only, returned in 1737, having triangulated 1 degree north of Tornio. 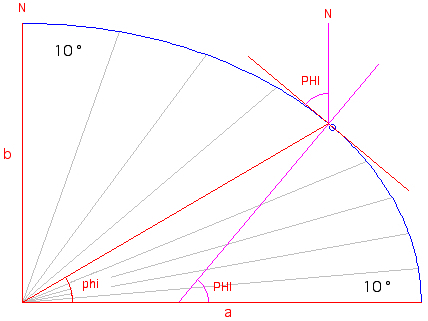 Flattening f = (a-b)/a = 0.3 = 1/3.33 The length of
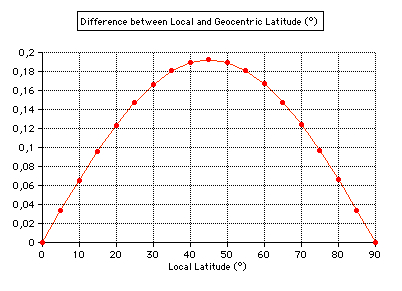
1 degree of meridian arc subtends a longer
distance in polar regions than near equato,
and the
geocentric latitude phi is smaller than the
local (true) latitude PHI. At sea level:
tan(phi)
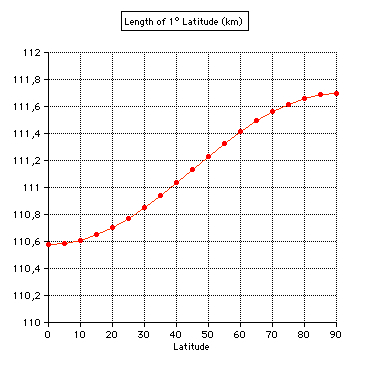
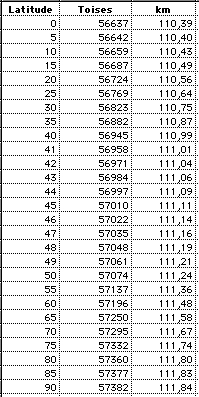
= (b/a)2 tan(PHI)The Results for 1° meridian arc measurements: using 1 Toise = 1.949.036 m
The figures
in the last column are computed using the
modern value of a= 6378.14 km.
The flattening adopted by the IAU in
1976 is f = 298.257.
Formula for the ratio of radii from Menke and Abbott: 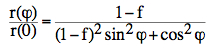 |
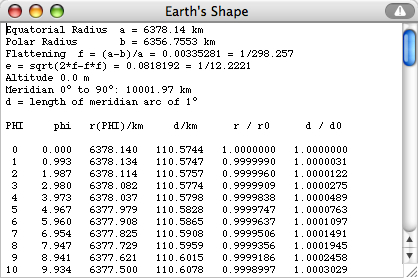
 Applet |
 Newtons "Principia" Book III, Propos. XX |
Assuming the Earth to be a rotating fluid in hydrostatic equilibrum the shape is approximately an ellipsoid: f = 1/299
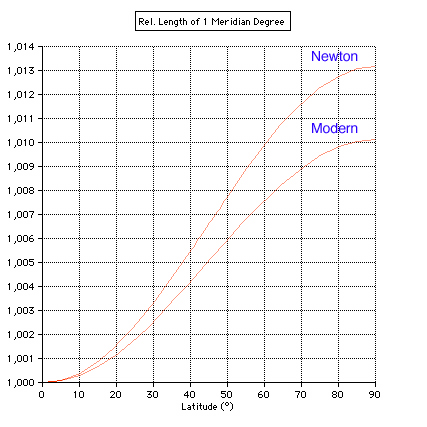
Newton: 1+0.006579*[1-cos(2*PHI)]
Modern: 1+0.005056*[1-cos(2*PHI)]
 Louis Godin 1704 - 1760 |
 Pierre Bouguer 1698 - 1758 |
 Charles Marie de La Condamine 1701 - 1774 |
| Source:
Wikipedia Commons |
||
The length of 1° determined by Google Earth compared with the applet values:
| Northern Latitude |
Google Earth |
Applet |
| 60° - 61° |
111.40 km |
111.42 km |
| 50° - 51° | 111.15 km | 111.24 km |
| 40° - 41° | 111.04 km | 111.04 km |
| 30° - 31° | 110.80 km | 110.86 km |
| 20° - 21° | 110.72 km | 110.71 km |
| 10° - 11° | 110.53 km | 110.61 km |
| 0° - 1° | 110.68 km | 110.57 km |
The circumference of the Earth: Eratosthenes and GPS
|
|
|
French Geodesic Mission (Wikipedia) H. K. Strick:
Maupertuis & La Condamine vermessen die Erde
(PDF) Figure of the
Earth (Wikipedia) The shape of the earth J. R Smith: The Meridian Arc
Measurement in Peru 1735 – 1745 (PDF) Eli Maor: Trigonometric Delights,
Chapter 5: Measuring Heaven and Earth (PDF) J.
R. Greenberg: The problem of the earth's shape
from Newton to Clairau Sir
Isaac Newton's Principia (Open Library) A
Earth Shape Applet (TU Clausthal) Quelle
est la forme de la Terre : plate, oblongue ou
aplatie aux pôles ? P.
Mohazzabi, Mark C. James: Plumb line and the shape
of the earth (PDF) |
| Books |
| William Menke, Dallas Abbott:
Geophysical theory, Columbia University Press, New
York/Oxford 1990. Jean Meeus: Astronomical Algorithms, Willmann-Bell, Chapter 10: The Earth's Globe. Paul Murdin: Die Kartenmacher - Der Wettstreit um die Vermessung der Welt, Artemis & Winkler, Mannheim 2010. Paul Murdin: Full Meridian of Glory - Perilous Adventures in the Competition to Measure the Earth, Springer Science, 2009. Robert Whitaker: Die Frau des Kartographen .. und das Rätsel um die Form der Erde, Karl Blessing, München 2005. Robert Whitaker: The Mapmaker's Wife. A True Tale of Love, Murder and Survival in the Amazon, Basic Books, New York 2004. Barbara Gretenkord (Hrsg.): Reise zur Mitte der Welt. Die Geschichte von der Suche nach der wahren Gestalt der Erde, Thorbecke, Ostfildern 2003. Florence Trystram: Le procès des étoiles - Récit de la prestigieuse expédition de trois savants français en Amérique du Sud et des aventure qui s'ensuivirent (1735-1771), Payot, Paris 2001. Florence Trystram: Der Prozess gegen die Sterne - Abenteuer einer Südamerika-Expedition, Brockhaus, Wiesbaden 1981. Michael Rand Hoare: The quest for the true figure of the Earth: Ideas And Expeditions In Four Centuries Of Geodesy, Ashgate Publishing, 2005. |
![]()
Updated:
2023, Oct 05